
A frustum is made by removing a small cone from a similar large cone. Work out the volume of the
A frustum is made by removing a small cone from a large cone. establish the volume The cones are mathematically similar. scallfacter The large cone has base radius rcm and height hcm. Given that ( volume of frustum )/( volume of large cone )=(98)/(125):0.784 find an expression, in terms of h, for the height of the frustum.

(PDF) Development of small scale frustum cone shaped butter churn
Paper 2 Higher - Sample Assessment Q22. Answers. 22) A frustum is made by removing a small cone from a large cone as shown in the diagram. The frustum is made from glass. The glass has a density of 2.5 g / cm3. Work out the mass of the frustum. Give your answer to an appropriate degree of accuracy. (5 marks)

[Solved] A frustum is made by removing a small cone from 9to5Science
The frustum is made by removing a small cone from a large cone. The cones are similar. h cm 2h cm r cm r cm Diagram NOT accurately drawn The height of the small cone is h cm. The height of the large cone is 2h cm. The radius of the base of the large cone is r cm. The radius of the sphere is r cm.
[Solved] A frustum is made by removing a small cone from 9to5Science
Question: a frustum is made by removing a small cone from a large cone. the cones are mathematically similar the cone has base radius r cm and height h cm given that volume of frustum/ volume of large cone = 98 / 125 find an expression, in terms of h, for the height of the frustum

A Frustum Is Made By Removing A Small Cone From A Similar Large Cone 38624 Hot Sex Picture
A frustum is made by removing a small cone from a large cone as shown in the diagram. The frustum is made from glass. The glass has a density of 2.5 g / cm 3. Work out the mass of the frustum. Give your answer to an appropriate degree of accuracy.

A frustum is made by removing a small cone from the top of a large cone. In the diagram shown
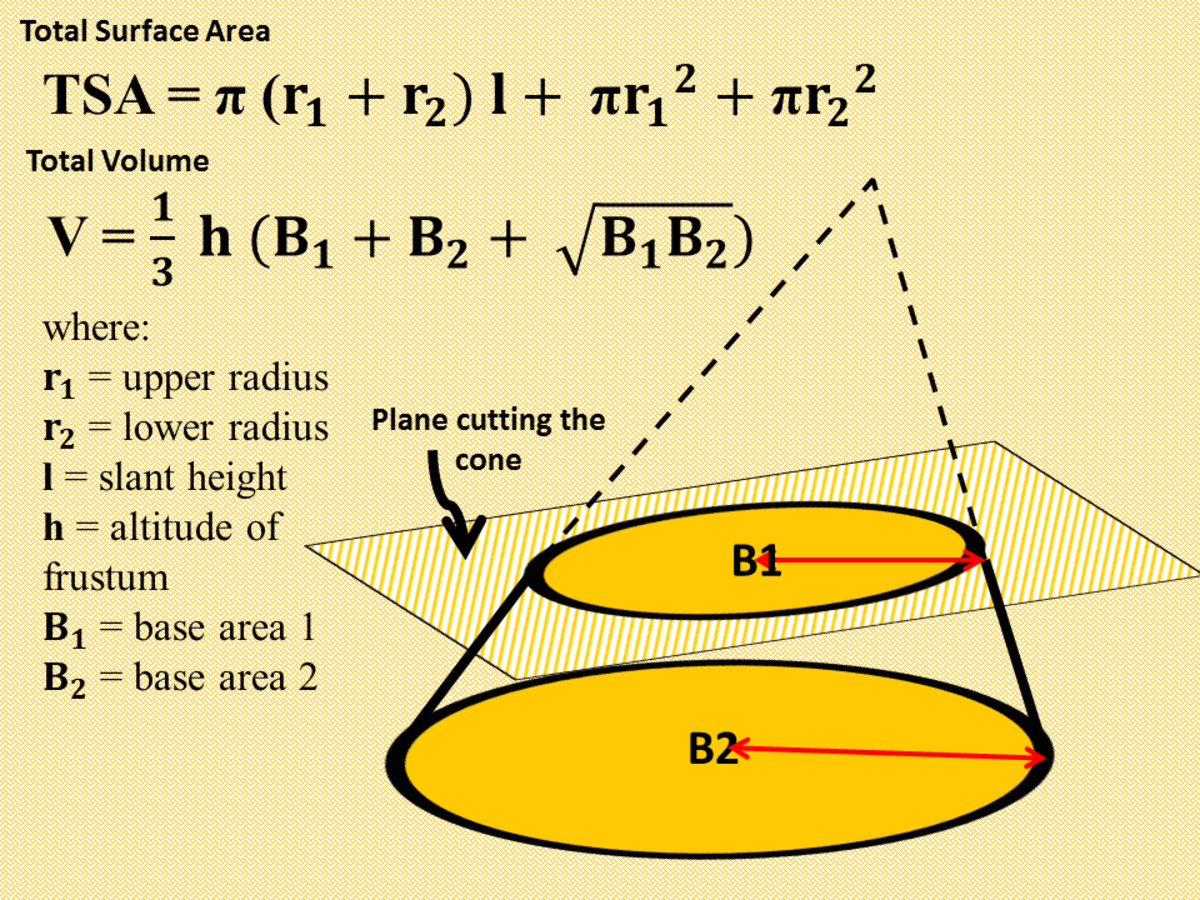
The height of frustum is 24m. If the height of the cone is 28m, then find the lateral surface area of frustum. Solution: Let, Radii are r1 = 10m and r2 = 3m. Height, h = 24m. First we need to find the slant height of frustum, by the formula: l = √ [ (r1 - r2)2 + h2] = √ { (10 - 3)2 + 242}
ブランド CONP 21AW Frustum of A Cone Bagの しますので
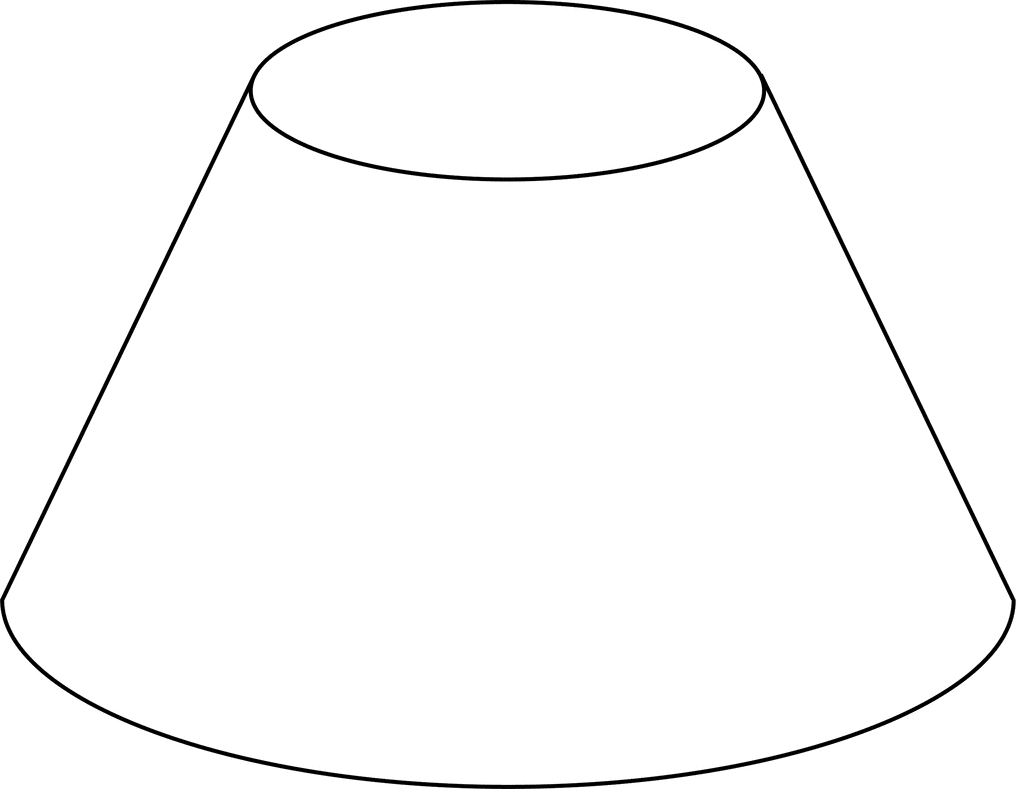
Frustums Example Questions. Question 1: Below is the frustum of a cone. The height of the cone is 50 cm, the radius of the base of the cone is 10 cm, and the height of the frustum is 30 cm. Work out the volume of the frustum to 3 significant figures. [3 marks] Question 2: Below is a frustum of a square-based pyramid.

Frustum of A Cone ClipArt ETC
A frustum is made by removing a small cone from a similar large cone. Work out the volume of the frustum, belo Get the answers you need, now!. Frustum of cone is the part of cone when it is cut by a plane into two parts. The upper part of cone remains same in shape but the bottom part makes a frustum.
Solved Here is a frustum of a cone. The diagram shows that the frustum is made by removing a
16 A frustum is made by removing a small cone from a large cone. The cones are mathematically similar. U cm Frustum h cm U cm Diagram NOT accurately drawn The large cone has base radius U cm and height h cm. Given that volume of frustum volume of large cone = 98 125 find an expression, in terms of h, for the height of the frustum.
Give two real life examples for a frustum of a cone
A frustum is made by removing a small cone from a large cone as shown in the diagram.. 1361 P1 process using similar triangles to find base of small cone, e.g. 4 cm used as diameter or 2 cm used as radius (d) P1 process to find volume of one cone (e) (f) P1 P1
Solved 6. Diagram I shows a shuttle cock, which is made up of two figures a hemispherical cap
Frustum. In geometry, a frustum ( Latin for 'morsel'); [a] ( pl.: frusta or frustums) is the portion of a solid (normally a pyramid or a cone) that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces are polygonal and the side faces are trapezoidal. A right frustum is a right pyramid or a right cone.

Frustum of a Cone ClipArt ETC
Given that the height of the small cone is a quarter of the height of the large cone, we can say that the small cone is 1/4 the size of the total cone. The volume of the frustum is worked out by subtracting the volume of the small cone from the volume of the large cone. It's important to understand that as the cones are similar, the radii of.

A frustum is made by removing a small cone from the top of a large cone. In the diagram shown
The frustum of a cone is the part of the cone without vertex when the cone is divided into two parts with a plane that is parallel to the base of the cone. Another name for the frustum of a cone is a truncated cone. Just like any other 3D shape, the frustum of a cone also has surface area and volume.We will see the formulas to find them in the upcoming sections.
Frustum of A Cone ClipArt ETC
Example Question. A frustum is made by removing a small cone from a similar large cone. The height of the small cone is 20 cm. The height of the large cone is 40 cm. The diameter of the base of the large cone is 30 cm. Work out the volume of the frustum. Give your answer correct to 3 significant figures.
Solved A frustum is made by removing a small cone from ≤ [algebra] Gauthmath
The frustum is made by removing a small cone from a large cone. The cones are similar. The height of the small cone is h cm. The height of the large cone is 2h cm. The radius of the base of the large cone is r cm. The radius of the sphere is r cm. Given that the volume of the frustum is equal to the volume of the sphere,
Solved 13 A frustum is made by removing a small cone from a large cone. The cones are
22 A frustum is made by removing a small cone from a large cone as shown in the diagram. The frustum is made from glass. g/cm 3 Work out the mass of the frustum. Give your answer to an appropriate degree of accuracy g (Total for Question 22 is 5 marks) TOTAL FOR PAPER IS 80 MARKS 10 cm 12 cm Volume of cone = 2 1 3 πr h h r PMT